MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.
MECÃNICA GRACELI GERAL - QTDRC.
equação Graceli dimensional relativista tensorial quântica de campos G* = = [ / IFF ] * * = / G / .= / G = [DR] = .= + + * * = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
| Teoria | Interação | mediador | Magnitude relativa | Comportamento | Faixa |
|---|---|---|---|---|---|
| Cromodinâmica | Força nuclear forte | Glúon | 1041 | 1/r7 | 1,4 × 10-15 m |
| Eletrodinâmica | Força eletromagnética | Fóton | 1039 | 1/r2 | infinito |
| Flavordinâmica | Força nuclear fraca | Bósons W e Z | 1029 | 1/r5 até 1/r7 | 10-18 m |
| Geometrodinâmica | Força gravitacional | gráviton | 10 | 1/r2 | infinito |
G* = OPERADOR DE DIMENSÕES DE GRACELI.
DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES DE CAMPOS E ENERGIAS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.
/
/ * *= = [ ] ω , , .=
MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE INTERAÇÕES DE CAMPOS. EM ;
MECÂNICA GRACELI REPRESENTADA POR TRANSFORMADA.
dd = dd [G] = DERIVADA DE DIMENSÕES DE GRACELI.
- [ G* /. ] [ [
G { f [dd]} ´[d] G* / . f [d] G* dd [G]
O ESTADO QUÂNTICO DE GRACELI
- [ G* /. ] [ []
G* = DIMENSÕES DE GRACELI TAMBÉM ESTÁ RELACIONADO COM INTERAÇÕES DE ENERGIAS, QUÂNTICAS, RELATIVÍSTICAS, , E INTERAÇÕES DE CAMPOS.
o tensor energia-momento é aquele de um campo eletromagnético,
/* = = [ ] ω , , .=
A equação para a energia do fóton[5] é
/ * = = [ ] , [ ] .=
Onde E é a energia do fóton, h é a constante de Planck, c é a velocidade da luz no vácuo e λ é o comprimento de onda do fóton. Como h e c são ambos constantes, a energia do fóton varia diretamente em relação ao comprimento de onda λ.
Para encontrar a energia do fóton em eV, usando o comprimento de onda em micrômetros, a equação é aproximadamente
/ * = = [ ] , [ ] .=
Portanto, a energia do fóton de comprimento de onda de 1 μm, próximo à da radiação infravermelho, é aproximadamente 1,2398 eV.
Como , onde f é a frequência, a equação da energia pode ser simplificada para
/ * = = [ ] , [ ] .=
Esta equação é conhecida como a relação de Planck-Einstein. Substituindo h por seu valor em J⋅s e f por seu valor em hertz resulta na energia do fóton em joules. Portanto, a energia do fóton à frequência de 1 Hz é 6,62606957×10−34 joules ou 4,135667516×10−15 eV.
Em química e engenharia óptica,
/ * = = [ ] , [ ] .=
é usada onde h é a constante de Planck e a letra grega ν (ni) é a frequência do fóton
Uma molécula típica, , possui vários níveis de energia diferentes. Quando uma molécula absorve um fóton, sua energia aumenta em uma quantidade igual à da energia do fóton. A molécula então entra em um estado excitado, .
Fótons no vácuo
No espaço vazio, conhecido como vácuo perfeito, todos os fótons se movem a velocidade da luz, c, determinada como sendo igual a 299 792 458 metros por segundo, ou aproximadamente 3×108 m s−1. O metro é definido como a distância percorrida pela luz no vácuo em 1/299 792 458 de um segundo, como a velocidade da luz não oferece qualquer incerteza experimental, diferente do metro ou do segundo, tanto que confiamos no segundo sendo definido por meio de um relógio muito preciso.
Segundo um princípio da relatividade restrita de Einstein, todas as observações da velocidade da luz no vácuo são as mesmas para todas as direções e para qualquer observador em um referencial inercial. Este princípio é geralmente aceito na física desde que muitas consequências práticas para as partículas de alta-energia tem sido observadas.
Fótons na matéria
Quando fótons passam através de material, tal como num prisma, frequências diferentes são transmitidas em velocidades diferentes. Isto é chamado de refração e resulta na dispersão das cores, onde fótons de diferentes frequências saem em diferentes ângulos. Um fenômeno similar ocorre na reflexão onde superfícies podem refletir fótons de várias frequências em diferentes ângulos.
A relação de dispersão associada para fótons é uma relação entre a frequência, f, e comprimento de onda, λ. ou, equivalentemente, entre sua energia, E, e momento, p. Isto é simples no vácuo, desde que a velocidade da onda, v, é dada por
As relações quânticas do fóton são:
- e
Onde h é constante de Planck. Então nós podemos escrever esta relação como:
que é característica de uma partícula de massa zero. Desta forma vemos como a notável constante de Planck relaciona os aspectos de onda e partícula.
Analisando o efeito fotoelétrico quantitativamente usando o método de Einstein, as seguintes equações equivalentes são usadas:
Energia do fóton = Energia necessária para remover um elétron + Energia cinética do elétron emitido
Algebricamente:
Onde:
- h é a constante de Planck,
- f é a frequência do foton incidente,
- é a função trabalho, ou energia mínima exigida para remover um elétron de sua ligação atômica,
- é a energia cinética máxima dos elétrons expelidos,
- f0 é a frequência mínima para o efeito fotoelétrico ocorrer,
- m é a massa de repouso do elétron expelido, e
- vm é a velocidade dos elétrons expelidos.
Notas:
Compton usou uma combinação de três fundamentais fórmulas representando os diversos aspectos da física clássica e moderna, combinando-os para descrever o procedimento quântico da luz[4].
- Luz como uma partícula;
- Dinâmica Relativística;
- Trigonometria.
O resultado final nos dá a equação do espalhamento de Compton:
Onde:
- é o comprimento de onda do fóton antes do espalhamento,
- é o comprimento de onda do fóton depois do espalhamento,
- me é a massa do elétron,
- é conhecido como o comprimento de onda de Compton,
- θ é o ângulo pelo qual a direção do fóton muda,
- h é a constante de Planck, e
- c é a velocidade da luz no vácuo.
Coletivamente, o comprimento de onda de Compton é .
Introduzida pela primeira vez em 1927 pelo físico alemão Werner Heisenberg,[2][3][4][5] a desigualdade formal que relaciona o desvio padrão da posição σx e o desvio padrão do momento σp foi derivada por Earle Hesse Kennard[6] mais tarde naquele ano e por Hermann Weyl[7] em 1928:
/ * = = [ ] , [ ] .= onde é a constante de Planck reduzida.
O princípio da incerteza essencialmente mecânica quântica vem em muitas formas além de posição-momento. A relação energia-tempo é amplamente usada para relacionar o tempo de vida do estado quântico a larguras de energia medidas, mas sua derivação formal é repleta de questões confusas sobre a natureza do tempo. O princípio básico foi estendido em várias direções; ele deve ser considerado em muitos tipos de medições físicas fundamentais.
Posição-momento

É vital ilustrar como o princípio se aplica a situações físicas relativamente inteligíveis, uma vez que é indiscernível nas escalas macroscópicas[8] que os humanos vivenciam. Duas estruturas alternativas para a física quântica oferecem explicações diferentes para o princípio da incerteza. A imagem da mecânica ondulatória do princípio da incerteza é mais intuitiva visualmente, mas a imagem mais abstrata da mecânica matricial o formula de uma forma que generaliza mais facilmente.
Matematicamente, na mecânica ondulatória, a relação de incerteza entre posição e momento surge porque as expressões da função de onda nas duas bases ortonormais correspondentes no espaço de Hilbert são transformadas de Fourier uma da outra (ou seja, posição e momento são variáveis conjugadas). Uma função diferente de zero e sua transformada de Fourier não podem ser nitidamente localizadas ao mesmo tempo.[9] Uma compensação semelhante entre as variâncias dos conjugados de Fourier surge em todos os sistemas subjacentes à análise de Fourier, por exemplo em ondas sonoras: um tom puro é um pico agudo em uma única frequência, enquanto sua transformada de Fourier dá a forma da onda sonora no domínio do tempo, que é uma onda senoidal completamente deslocalizada. Na mecânica quântica, os dois pontos-chave são que a posição da partícula assume a forma de uma onda de matéria, e o momento é seu conjugado de Fourier, assegurado pela relação de Broglie p = ħk, onde k é o número de onda.
Na mecânica matricial, a formulação matemática da mecânica quântica, qualquer par de operadores autoadjuntos não comutativos representando observáveis estão sujeitos a limites de incerteza semelhantes. Um autoestado de um observável representa o estado da função de onda para um certo valor de medição (o autovalor). Por exemplo, se uma medição de um observável A for realizada, então o sistema está em um autoestado particular Ψ daquele observável. Entretanto, o autoestado particular do observável A não precisa ser um autoestado de outro observável B: Se for, então ele não tem uma medição única associada a ele, pois o sistema não está em um autoestado daquele observável.[10]
Visualização
O princípio da incerteza pode ser visualizado usando as funções de onda de posição-espaço e de momento-espaço para uma partícula sem spin com massa em uma dimensão.
Quanto mais localizada a função de onda de posição-espaço, mais provável é que a partícula seja encontrada com as coordenadas de posição naquela região e, correspondentemente, a função de onda de momento-espaço é menos localizada, de modo que os possíveis componentes de momento que a partícula poderia ter são mais difundidos. Por outro lado, quanto mais localizada a função de onda de momento-espaço, mais provável é que a partícula seja encontrada com aqueles valores de componentes de momento naquela região e, correspondentemente, menos localizada a função de onda de posição-espaço, de modo que as coordenadas de posição que a partícula poderia ocupar são mais difundidas. Essas funções de onda são transformadas de Fourier uma da outra: matematicamente, o princípio da incerteza expressa a relação entre variáveis conjugadas na transformada.
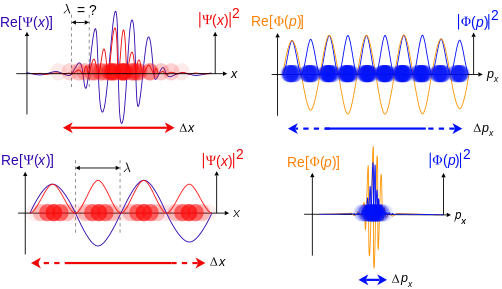
Topo: Se o comprimento de onda λ for desconhecido, o momento p, o vetor de onda k e a energia E também o são (relações de Broglie). Como a partícula é mais localizada no espaço de posição, Δx é menor do que para Δpx.
Embaixo: Se λ for conhecido, p, k e E também o são. Como a partícula é mais localizada no espaço de momento, Δp é menor do que para Δx.
Interpretação da mecânica ondulatória
De acordo com a hipótese de de Broglie, todo objeto no universo está associado a uma onda. Assim, todo objeto, de uma partícula elementar a átomos, moléculas e planetas e além, está sujeito ao princípio da incerteza.
A função de onda independente do tempo de uma onda plana monomodo de número de onda k0 ou momento p0 é:
A regra de Born afirma que isso deve ser interpretado como uma função de amplitude de densidade de probabilidade no sentido de que a probabilidade de encontrar a partícula entre a e b é:
No caso da onda plana monomodo, é 1 se e 0 caso contrário. Em outras palavras, a posição da partícula é extremamente incerta no sentido de que ela poderia estar essencialmente em qualquer lugar ao longo do pacote de ondas.
Por outro lado, considere uma função de onda que é uma soma de muitas ondas, que podemos escrever como:
onde An representa a contribuição relativa do modo pn para o total geral. As figuras à direita mostram como com a adição de muitas ondas planas, o pacote de ondas pode se tornar mais localizado. Podemos levar isso um passo adiante para o limite do contínuo, onde a função de onda é uma integral sobre todos os modos possíveis:
com representando a amplitude desses modos e é chamada de função de onda no espaço de momento. Em termos matemáticos, dizemos que é a transformada de Fourier de e que x e p são variáveis conjugadas. Adicionar todas essas ondas planas tem um custo, ou seja, o momento se tornou menos preciso, tendo se tornado uma mistura de ondas de muitos momentos diferentes.[11]
Uma maneira de quantificar a precisão da posição e do momento é o desvio padrão σ. Como é uma função de densidade de probabilidade para posição, calculamos seu desvio padrão.
A precisão da posição é melhorada, ou seja, σx reduzido, usando muitas ondas planas, enfraquecendo assim a precisão do momento, ou seja, σp aumentado. Outra maneira de afirmar isso é que σx e σp têm uma relação inversa ou são pelo menos limitados por baixo. Este é o princípio da incerteza, cujo limite exato é o limite de
 =
=
 /
/ 
 G
G 













 ]
]
























![{\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}|\psi (x)|^{2}\,\mathrm {d} x~}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2187e81db11de0ff80dab3cfeaed71231b213bdd)






Comments
Post a Comment